Cartier Divisors are a geometer’s husband and Weil Divisors are her* paramour

As is necessary, we start this writing by a discussion on regular elements in a commutative ring (denoted by the capital letter A). We are so used to working with the real or complex numbers that whenever we see ab=0 for two numbers a and b, we are tempted to immediately conclude that a=0 or b=0. This is not the case if we work with a general commutative ring, i.e. a general number system with addition and multiplication. As this conclusion may fail for some commutative rings, we would like to differentiate the elements for which this conclusion is true by calling them regular, i.e. a nonzero element a is regular if ab=0 implies that b=0.

Let us now discuss a bit about the distinction between geometry and topology. You might think a topological object as a shape whereas a geometric object is a shape equipped with a class of functions. So, geometric objects by definition carry extra data. An interested reader might look up the definition of a locally ringed space and get a clear idea what is actually meant by this extra data. Let us now take a particular kind of geometric object called a scheme. It is such an object that is glued from the pieces made of commutative rings and this pieces will be called affine open subsets. The correspondence between commutative rings and the so-called affine schemes is the most beautiful work in Mathematics during the 20th century due to Alexander Grothendieck. But, we will postpone this discussion to another writing.

(1) Genus two algebraic curve

An effective Cartier divisor on a scheme is a collection of pairs of affine open subsets and regular elements where the open subsets appearing in this collection covers the whole scheme and these regular elements (whenever we can compare) differ by an invertible element. You might think about these regular elements as fancy and abstract functions defined on the affine open subset that they are paired with. With this point of looking at regular elements as functions, you would believe me that we can consider the zero set of these (local) regular elements on the scheme and the union of such zero subsets gives us a codimension 1 closed subset of the scheme. Moreover, this zero subset (rather its irreducible components) can be equipped with an integer called a multiplicity . This leads to a definition of a Weil divisor. A Weil divisor on a (Noetherian) scheme is a finite union of codimension 1 irreducible closed subsets, each of which is equipped with some multiplicity …,-3,-2,-1,1,2,3,…

There is a way of identifying certain Weil divisors to get a manageable invariant of a scheme. For this purpose, we will define (global) invertible meromorphic functions on a scheme. They are a coherent collection of fractional functions of affine open subsets, i.e. collections of functions of the from a/b where a and b are regular functions and they glue to a global element. Each global, invertible meromorphic function can be regarded as a (possibly noneffective) Cartier divisor, hence we can associate a Weil divisor to it. We call those Weil divisors that come from a meromorphic function principal. Here comes the star object of this writing: Take the quotient of the (group) of Weil divisors by the (subgroup) of principal Weil divisors and the resulting group is called the class group Cl(X) of the scheme X under consideration.

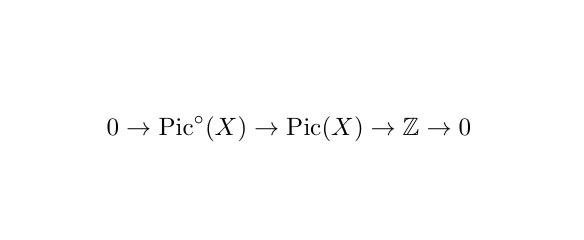
(2) Short exact sequence of a Picard group

Let’s wrap up this discussion with a computation. Let us take an elliptic curve (a torus equipped with algebraic functions and a distinguished point e). As it is a curve i.e. a 1-dimensional scheme, its codimension 1 closed subsets are of dimension 0, namely a finite number of points. Remember that as Weil divisors, these points are equipped with integers. Elliptic curves are so special objects that if we take two points x, y on an elliptic curve, we can get a unique third point z (that is the “addition of x and y”). Inside the class group, the Weil divisor x+y becomes equivalent to the Weil divisor z+e (here e is the distinguished point). This shows that any finite union of points with positive multiplicity can be reduced to a Weil divisor of the from w+ne for some point w and a positive integer n. It also shows that the Weil divisor x plus the inverse (denoted by t) of x (with respect to the “addition” on the elliptic curve) is equivalent to 2e. Playing around, we get that the (noneffective) Weil divisor -x is equivalent to t-2e (here again t denotes the inverse of x). That said, any (effective or not) Weil divisor can be represented (inside the class group) by some Weil divisor w+ne where w is a point and n is a (possibly negative) integer. It requires more argument that this representation is in fact unique. I.e. elements of the class group of an elliptic curve are pairs of a (closed) point on the elliptic curve and an integer. We started with an elliptic curve and “recovered” it as an invariant. Given that an elliptic curve is a geometric object that has the structure of a group (compatible with its geometry), we had to put quotation marks around the word recover. A justification of this word would lead us to the notion of Jacobian (a topic of another future writing). A careful reader who knows about group theory should now figure out the group structure on the class group of an elliptic curve. (Hint: the true answer might not be your first guess and you can look at the sequence above for an idea)

Author’s note:
*We prefer being politically correct by designating geometers as females.
The author learned algebraic geometry from Qing Liu’s lovely book “Algebraic Geometry and Arithmetic Curves”. It only makes sense to include his book in the references.

References: Liu, Qing. Algebraic Geometry and Arithmetic Curves. https://books.google.com/books/about/Algebraic_Geometry_and_Arithmetic_Curves.html?id=ePpzBAAAQBAJ&printsec=frontcover&source=kp_read_button

Photos: (1) https://blogs.ams.org/visualinsight/files/2016/08/genus_two_curve.png Access date: 30 January 2019
(2) Created using LATEX